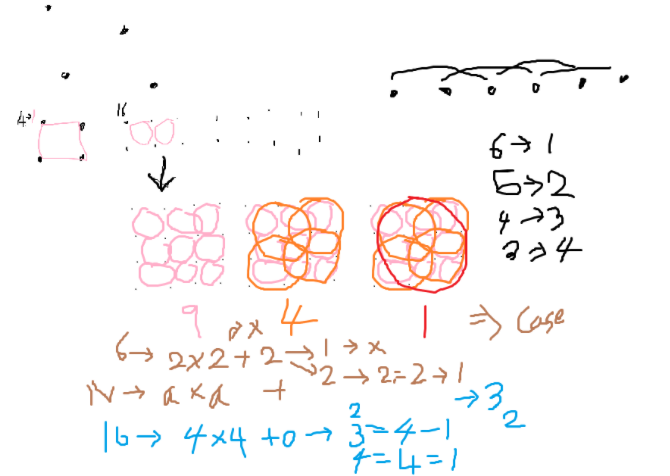
마우스로도 쌈뽕하게 그릴 수 있을 줄 알았지만 전혀 아니었다. 원래 처음에 푸는 거 공유하는 맛이라 정신승리했지만 다시보니 그림판은 너무 선넘었다.. 문제풀이 공유스터디 첫날에 쫓겨날 판이다. 앞으로는 태블릿을 사용해야지.
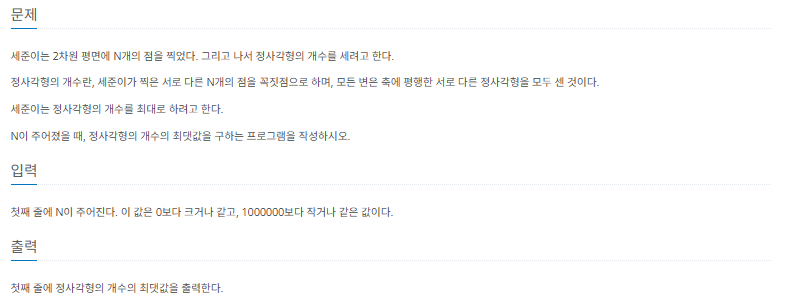
2차원 평면의 정사각형 개수의 최댓값을 구하는 문제다. 조건은 딱히 얻어갈 것은 없고 1개 이상이다. 일단 정사각형을 하나 만들기 위해 최소한이 4개 이기 때문에 1~3개의 케이스인 경우 0을반환해야 한다.
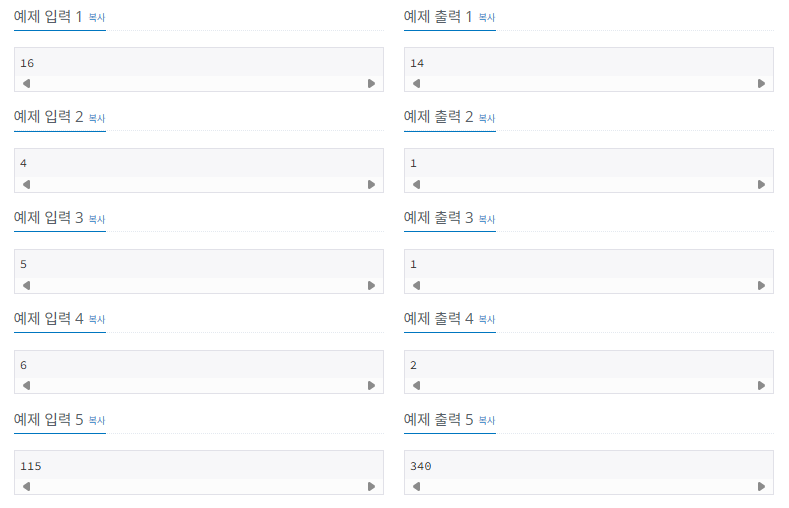
일단 가장 작은 값으로 문제를 이해해했다.

사실 처음에 문제 제대로 안읽어서 이따구로 점찍어놓고 정사각형이 어떻게 되는가를 고민했다. 바보..
4는 일단 예의상 그려줬다.
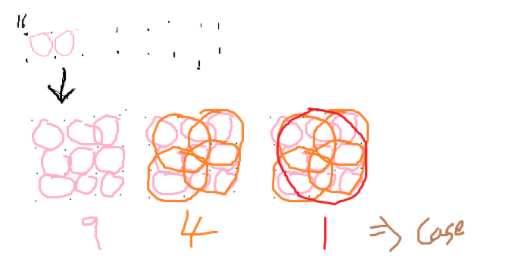
처음에는 점을 어떻게 놔야 최댓값을 구할 수 있는지 생각안하고 일단 옆으로 길게 놨다가 최대한 공통변을 이용해야 최댓값이 나올 듯하여 수정했고, 각각의 케이스에 따라 판단해야 한다는 것을 이해할 수 있었다.
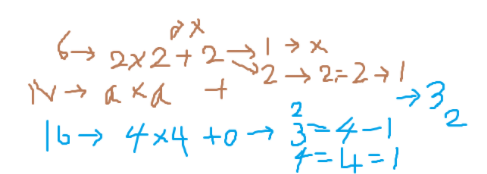
이걸 변수화해보면, N은 어떤 수 a의 제곱보다 큰 값이 들어가야 한다. 6의 케이스를 살펴보면 2의 제곱인 4와 나머지 2로 된다. 일단 나머지가 없는 제곱수만 계산해보겠다
이제 변으로 사용되는 점의 케이스를 계산해야한다. 일단 길이가 1인 정사각형은 (a - 1)의 제곱, 2인 정사각형은 (a-2)의 제곱으로 (a - 1)까지 계산한다. 최종적으로 그걸 다 더하면 정사각형의 개수가 나온다.
function countSquares(N) {
if (N < 4) return 0;
let totalSquares = 0;
let a = Math.floor(Math.sqrt(N));
for (let i = 1; i <= a; i++) {
totalSquares += (a - i) ** 2;
}
return totalSquares;
}
console.log(countSquares(16)); // 14
console.log(countSquares(8)); // 1
자바스크립트로 풀어놓으면 이렇게 되는데, 내가 푼게 베스트 케이스만 골라잡은 것이다. 역시 골드 3은 쉽지 않다
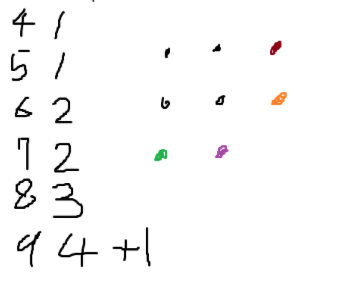

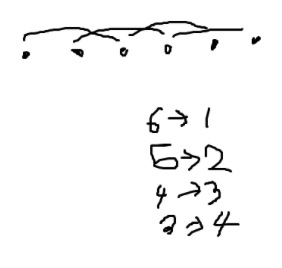
??
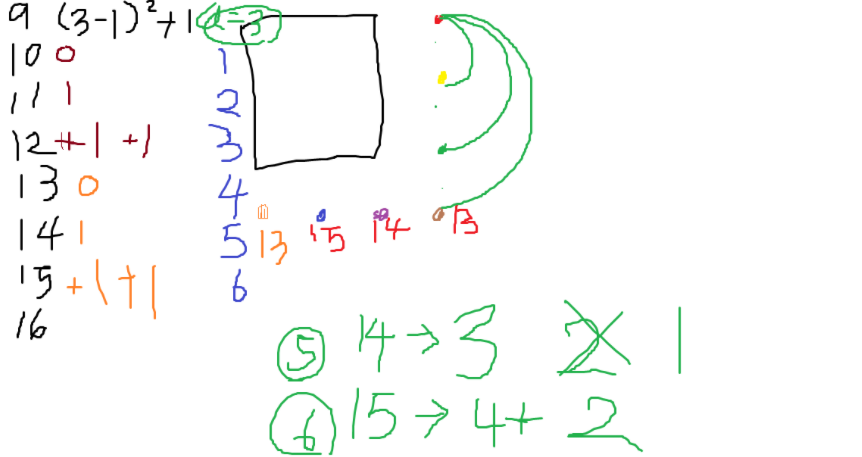
너무 안 찾아져서 다시 찾으면서 봤더니,, 나머지 수가 a - 1이 되면 반대편으로 넘어가야 최댓값이 나왔다..
그래서 나머지 수 가지고 1부터 a - 1까지의 경우의 수를 더해줘야 했다.

아니었다.
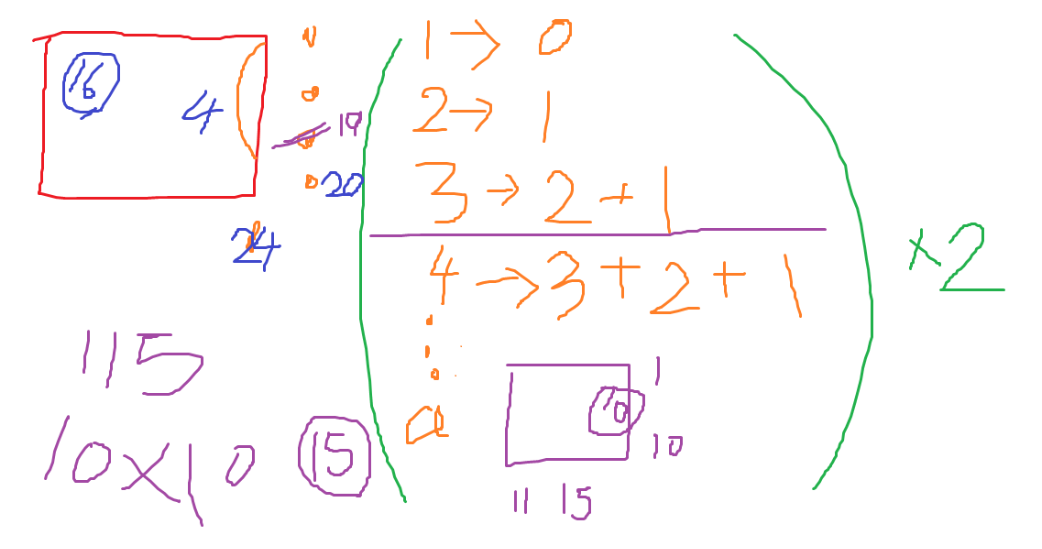
115에서 에러가 생기길래, 16 이상으로 케이스를 계산해봤다. 나머지가 a보다 작은 경우 높이를 1부터 나머지를 더해 계산해주고, a를 넘어가는 경우 나머지에서 a를 제거하고 나머지까지를 더해서 해결했다.
function countSquares(N) {
if (N < 4) return 0;
let totalSquares = 0;
let a = Math.floor(Math.sqrt(N));
for (let i = 1; i <= a; i++) {
totalSquares += (a - i) ** 2;
}
let restDots = N - a * a;
if (restDots === 0) return totalSquares;
if (restDots <= a) {
for (let i = 1; i <= restDots - 1; i++) {
totalSquares += i;
}
} else {
for (let i = 1; i <= a - 1; i++) {
totalSquares += i;
}
for (let i = 1; i <= (restDots - a) - 1; i++) {
totalSquares += i;
}
}
return totalSquares;
}
console.log(countSquares(4)); // 1
console.log(countSquares(5)); // 1 // 1
console.log(countSquares(6)); // 2 // 2 (2)
console.log(countSquares(16)); // 14 // 0
console.log(countSquares(115)); // 340 // 15 (10)
'코딩테스트' 카테고리의 다른 글
| 백준 14939번 불 끄기 자바스크립트 (2) | 2024.07.14 |
|---|---|
| 백준 2239번 정사각형의 개수 자바스크립트 (0) | 2024.07.07 |
| 효율적인 렌더링을 위한 렌더링 최적화 (0) | 2023.09.18 |